Accueil > Publications > Roulement sans glissement.

Roulement sans glissement.

Comment interpréter l’hypothèse "Rouler sans glisser" ?

dimanche 28 août 2016, par ScientificWare

.
Objectif : Montrer que pour tout point de coordonnées polaires $(\rho,\theta)$ appartenant à une cardioïde $\rho=2R(1+cos\theta)$ .

Je soumets ici ma réflexion aux regards de ceux qui pourraient apporter des corrections ou des simplifications. Car il est possible que je sois passé à côté de quelque chose de plus simple.
"Rouler sans glisser" !
J’avais et j’ai passé beaucoup de temps à essayer d’interpréter cette hypothèse qui pour moi n’avait rien d’évidente. Après quelques semaines de réflexion et finalement 4 jours en août, je me suis rappelé que cette notion devait être définie dans le cours de mécanique :
On fait intervenir la vitesse de glissement $\vec V_{1/2}$ d’une surface sur une autre relativement à un référentiel .
Elle est définie par $\vec{V}_{1/2}=\vec{V}_{I_1/R}-\vec{V}_{I_2/R}$ .
$I_{1}$ et $I_{2}$ sont respectivement les points de et en contact, $\vec{V}_{I_1/R}$ et $\vec{V}_{I_2/R}$ leur vitesse dans .
Si $\vec{V}_{1/2}=\vec{0}$ , il n’y a pas glissement sinon, il y a glissement.
Pour travailler, j’ai besoin de deux référentiels, $R(\vec{i},\vec{j})$ et $R^{\prime}(\vec{m},\vec{n})$ avec deux bases unitaires directes.
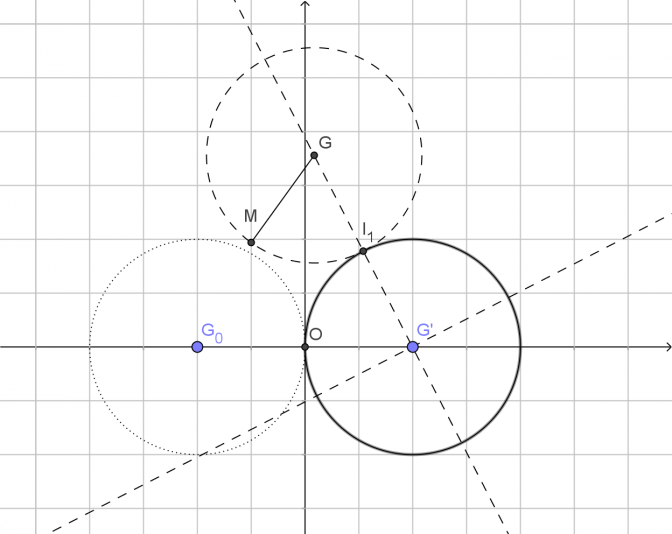
Le cercle immobile est $C_{2}$ de centre $G^{\prime}$ , $R^{\prime}$ lui est associé.
Le cercle qui roule est $C_{1}$ de centre , lui est associé.
En coordonnées polaires $G(2R,\alpha)_{R^{\prime}}$ et $G(R,\beta)_R$
(Ensuite dire que le cercle cercle $C_{1}$ roule sur $C_{2}$ ne me parait pas suffisant, je rajoute qu’il doit avoir une vitesse angulaire constante. [Remarque à supprimer car rien ne justifie d’imposer une vitesse Constante]).
C’est à dire ${\dot{\beta}}$ constant [Remarque à supprimer car rien ne justifie d’imposer une vitesse Constante].
Puisqu’il n’y a pas glissement et que $C_{2}$ est immobile $\vec{V}_{1/2}=\vec{0}$ est équivalent à $\vec{V}_{I_1/R^{\prime}}=\vec{0}$ .
En dérivant dans $R^{\prime}$ chaque membre de $\overrightarrow{G^\prime I_1}=\overrightarrow{G^{\prime}G}+\overrightarrow{GI_1}$ , on arrive à l’égalité :
$2 \dot{\alpha} =\dot{\beta}$ .
Autement dit, la vitesse angulaire de dans $R^{\prime}$ est aussi constante [Remarque à supprimer car rien ne justifie d’imposer une vitesse Constante].
Voilà, c’est le résultat que me manquait.
Ensuite, je reprends comme dans la correction.
En notant $\overrightarrow{OM}=\overrightarrow{OG^{\prime}}+\overrightarrow{G^\prime G}+\overrightarrow{GM}$ avec leur affixe dans $R^{\prime}$ , nous obtenons :
$\rho e^{i\theta}=R+2Re^{i(\dot\alpha t+\pi)}+Re^{i \dot\beta t}$ , ${\pi}$ est introduit simplement pour respecter les conditions initiales à .
$\rho e^{i\theta}=R+2Re^{i(\dot\alpha t+\pi)}+Re^{i 2 \dot\alpha t}$ puisque $\dot{\beta}=2 \dot{\alpha}$ .
Mais on peut également écrire $\rho e^{i \theta}=R+2Re^{i(\dot\alpha t+\pi)}+Re^{i(2\dot\alpha t +2\pi)}$ .
On factorise le second membre par $Re^{i(\dot{\alpha} t+\pi)}$ pour obtenir :
$\rho e^{i \theta}=2R(1+cos(\dot\alpha t+\pi))e^{i(\dot\alpha t+\pi)}$ car $e^{i(\dot\alpha t+\pi)}+e^{-i(\dot\alpha t+\pi)}=2cos(\dot\alpha t+\pi)$
Par identification $\theta=\dot\alpha t+\pi$ et $\rho=2R(1+cos\theta)$ .
Qu’en pensez-vous ?